９．ソーティング（ヒープソート）

９．１．ヒープソート

選択ソートとバブルソートは計算量がO(n²) （計算量がデータ数の2乗に比例する）で実行時間が非常にかかるので、実際にはほとんど使用されません。ここでは計算量がO(nlogn) ですむ「ヒープソート」を解説します。

「ヒープ」とは２分木（1つの節から伸びる枝の本数が2本以下である木）で、自分の値が子の値よりも必ず大きい（小さい）ものを言います。下図は自分の値が子の値よりも必ず小さいヒープです。

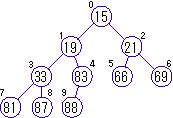
上図のように節および根に番号をふったヒープを配列で表現すると、a[n]の子はa[2n+1]とa[2n+2]、a[n]の親はa[(n-1)/2]となります。

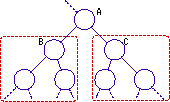
自分の値が子の値よりも必ず小さいヒープの作成方法について説明します。ここで下図のようなAを根とする部分木を考えます。BおよびCを根とする部分木は既にヒープになっているとします。この状態でAにあるデータαに対して以下の操作を繰り返すと、Aを根とする部分木全体もヒープになります。

つまり「αが2つの子のデータと比較して、一番小さくないならば入れ替え」という処理を、子供がいなくなるか終了するまで繰り返します。

最初はどの部分木もヒープではありませんが、一番末端の右端にある部分木（９．１の図の場合は「4」を根とする部分木）から順に上記の処理を実行していけば、木全体がヒープになります。

ヒープができても、ソーティングはまだ完成していません。「９．１」の図はヒープですが、配列内のデータは順番に並んでいません。ヒープからデータを順番に並べるためには次のようにします。

ヒープでは根にあるデータが最も小さいので、このデータを取り除きます。そして空いた根の部分に、最も末端の右端にあるデータを移してきます。「９．１」図の場合は、9のデータ「88」を0に移すので、以下のようになります。

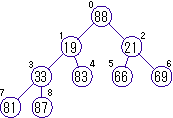
この状態は「９．２」図と同じ状態で、１および２を根とする部分木はヒープになっていますが、全体はヒープになっていません。これに対して「９．２」と同じ処理を繰り返すと再びヒープになります。

この処理をデータがなくなるまで繰り返していくと、データを小さい順に取り出していくことができます。これがヒープソートのアルゴリズムです。

以下のプログラムを作成しなさい。

　1　2