こんにちは、桂川です。本記事では、Rによるデータ分析について超入門的な内容を紹介します。特に、可視化について紹介します。Rとは、オープンソースソフトウェアであり、プログラミング言語の一種です。Rの特徴として、統計解析やデータ分析に特化しているという点が挙げられます。具体的には、統計解析やデータ分析、機械学習の役に立つライブラリや関数が充実しています。このような特徴をもつRを利用して、データ分析を試してみます。
Rによるデータの可視化
概要
本記事では、Rを利用してオープンデータを分析します。 特に、データ全体の概要を読み解くために、データの可視化に取り組みます。
今回、設定した目的は「家の価格に大きい影響をもつ特徴の把握」です。 個人的な話になりますが、新入社員としての目標は良い家に住むことです。しかし、様々な特徴で価格は変わっていきます。例えば以下の特徴です。
- 部屋の数はいくつにするのか
- 外見はどれほどこだわるのか
- 海が見える水辺に建てるのか
これらの特徴はこだわりの強い自分にとって、とても重要かつ把握しておくべき内容かと思い（少々気が早いですが）調査してみます。
対象とするデータの詳細
本記事では、オープンデータとして公開されている住宅価格情報*1 を利用してそれらの特徴を分析します。このデータを可視化することで、住宅価格に特に大きい影響を与える特徴を把握する手がかりを発見できるかもしれません。
データサイエンスに関するコニュニティーサイト「Kaggle」から今回の分析に利用する[住宅価格情報（kc_data.csv）」をダウンロードします。
データの可視化
対象データの把握
まずは、対象とするデータがどのようなものなのか実際に見てみます。以下のコードを実行することによりcsvファイルの内容を表形式で標準出力できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 利用するライブラリをあらかじめインポートします。 library(ggplot2) library(readr) library(RColorBrewer) library(dplyr) library(gridExtra) library(corrplot) library(caret) library(ggmap) library(tidyverse) library(moderndive) # まずは、データセット（csvファイル）を読み込みます。 data <- read.csv("kc_data.csv", stringsAsFactor=F) # headにより、表の上から6件のみを表示させることができます。 head(data) |
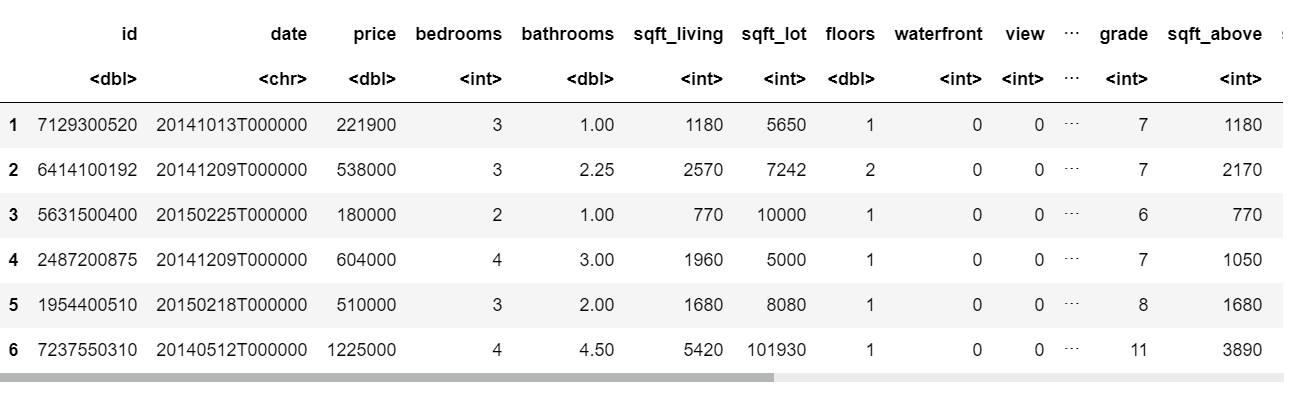
これで、csvファイルの内容が把握できます。このcsvデータは列数（IDを含めた変数の数）は21列、行数は約2万行でした。
基本統計量の出力
今回のデータにはどのような特徴があるのか、2万行あるこの表を目視で確認することは気の遠くなる作業なので、各列の基本統計量を算出します。基本統計量とは、データの基本的な特徴を表すものです。例えば、以下のようなものが挙げられます。
- Min. : 最小値
- 1st Qu. : 第１四分位
- Median : 中央値
- Mean : 平均値
- 3rd Qu. : 第３四分位
- Max. : 最大値
R では summaryを呼びだす事で、指定されたデータについて、上記を取得して出力します。これによりデータの概要を把握できます。
以下のコードを実行することで、データの基本統計量を標準出力できます。
|
1 2 |
# summaryによって要約されたデータを見ることができます。 summary(data) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
id date price bedrooms Min. :1.000e+06 Length:21613 Min. : 75000 Min. : 0.000 1st Qu.:2.123e+09 Class :character 1st Qu.: 321950 1st Qu.: 3.000 Median :3.905e+09 Mode :character Median : 450000 Median : 3.000 Mean :4.580e+09 Mean : 540088 Mean : 3.371 3rd Qu.:7.309e+09 3rd Qu.: 645000 3rd Qu.: 4.000 Max. :9.900e+09 Max. :7700000 Max. :33.000 bathrooms sqft_living sqft_lot floors Min. :0.000 Min. : 290 Min. : 520 Min. :1.000 1st Qu.:1.750 1st Qu.: 1427 1st Qu.: 5040 1st Qu.:1.000 Median :2.250 Median : 1910 Median : 7618 Median :1.500 Mean :2.115 Mean : 2080 Mean : 15107 Mean :1.494 3rd Qu.:2.500 3rd Qu.: 2550 3rd Qu.: 10688 3rd Qu.:2.000 Max. :8.000 Max. :13540 Max. :1651359 Max. :3.500 waterfront view condition grade Min. :0.000000 Min. :0.0000 Min. :1.000 Min. : 1.000 1st Qu.:0.000000 1st Qu.:0.0000 1st Qu.:3.000 1st Qu.: 7.000 Median :0.000000 Median :0.0000 Median :3.000 Median : 7.000 Mean :0.007542 Mean :0.2343 Mean :3.409 Mean : 7.657 3rd Qu.:0.000000 3rd Qu.:0.0000 3rd Qu.:4.000 3rd Qu.: 8.000 Max. :1.000000 Max. :4.0000 Max. :5.000 Max. :13.000 sqft_above sqft_basement yr_built yr_renovated Min. : 290 Min. : 0.0 Min. :1900 Min. : 0.0 1st Qu.:1190 1st Qu.: 0.0 1st Qu.:1951 1st Qu.: 0.0 Median :1560 Median : 0.0 Median :1975 Median : 0.0 Mean :1788 Mean : 291.5 Mean :1971 Mean : 84.4 3rd Qu.:2210 3rd Qu.: 560.0 3rd Qu.:1997 3rd Qu.: 0.0 Max. :9410 Max. :4820.0 Max. :2015 Max. :2015.0 zipcode lat long sqft_living15 Min. :98001 Min. :47.16 Min. :-122.5 Min. : 399 1st Qu.:98033 1st Qu.:47.47 1st Qu.:-122.3 1st Qu.:1490 Median :98065 Median :47.57 Median :-122.2 Median :1840 Mean :98078 Mean :47.56 Mean :-122.2 Mean :1987 3rd Qu.:98118 3rd Qu.:47.68 3rd Qu.:-122.1 3rd Qu.:2360 Max. :98199 Max. :47.78 Max. :-121.3 Max. :6210 sqft_lot15 Min. : 651 1st Qu.: 5100 Median : 7620 Mean : 12768 3rd Qu.: 10083 Max. :871200 |
各変数について、どのような分布なのか、分かりやすくなりました。例えば、今回のデータでは、価格（price）は75, 000～7700, 000の間の値をとり、平均値は540, 088、中央値は450, 000 である事が分かります。また 階の数（floors）については、1～3.5 の間で、中央値は1.5ということが分ります。
ヒストグラムの描画
ただし、この数値を見てもまだまだ分かりにくい・・・直感的ではない・・・特徴の把握が難しい・・・ということで、これらを可視化していきましょう。まずは価格について見ていきます。今回はヒストグラムにしてみます。ヒストグラムとは、縦軸に度数、横軸に階級をとった統計グラフの一種で、データの分布の状況を視覚的に認識するために利用されます。
以下のコードを実行することで、ヒストグラムの描画ができます。
|
1 2 3 4 5 |
options(scipen=999) options(repr.plot.width=20, repr.plot.height=20, align="center") g2 <- ggplot(data, aes(x=price))+geom_histogram(fill="blue") g2 |
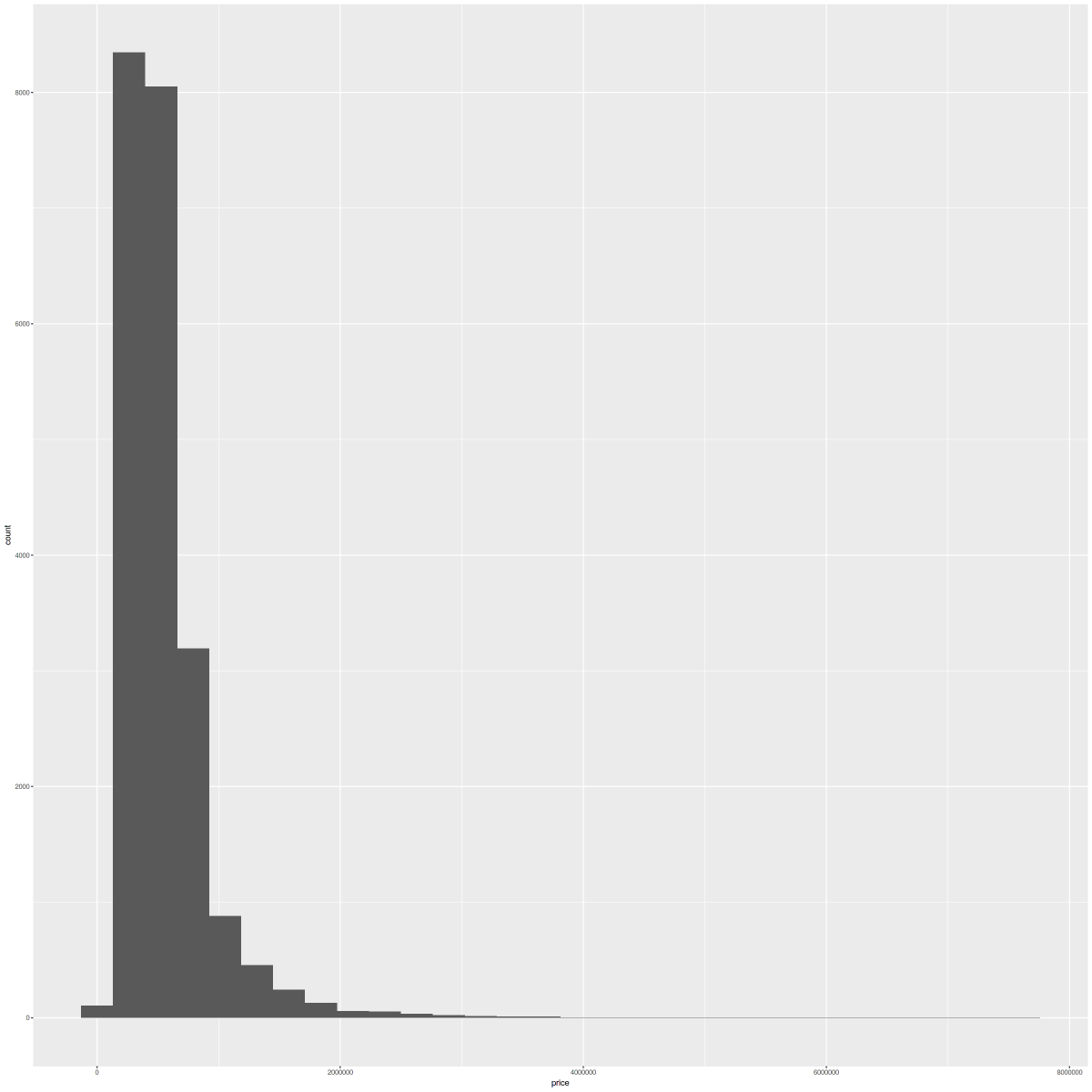
横軸が家の価格、縦軸がその価格の家の数です。可視化したことにより、分布が直感的でわかりやすくなりましたね。ほとんどの値が、500, 000~750, 000あたりのようです。
ただし、このような極端な分布を表すヒストグラムでは、細かい特徴を認識することは難しそうです。このような場合は、値を対数logに変換するなどして、わかりやすくすることもできます。今回は価格のみ試してみます。
以下のコードを実行することで、対数変換した値のヒストグラムの描画ができます。
|
1 2 3 |
data<-mutate(data, log_price=log10(price)) g2 <- ggplot(data, aes(x=log_price))+geom_histogram() g2 |
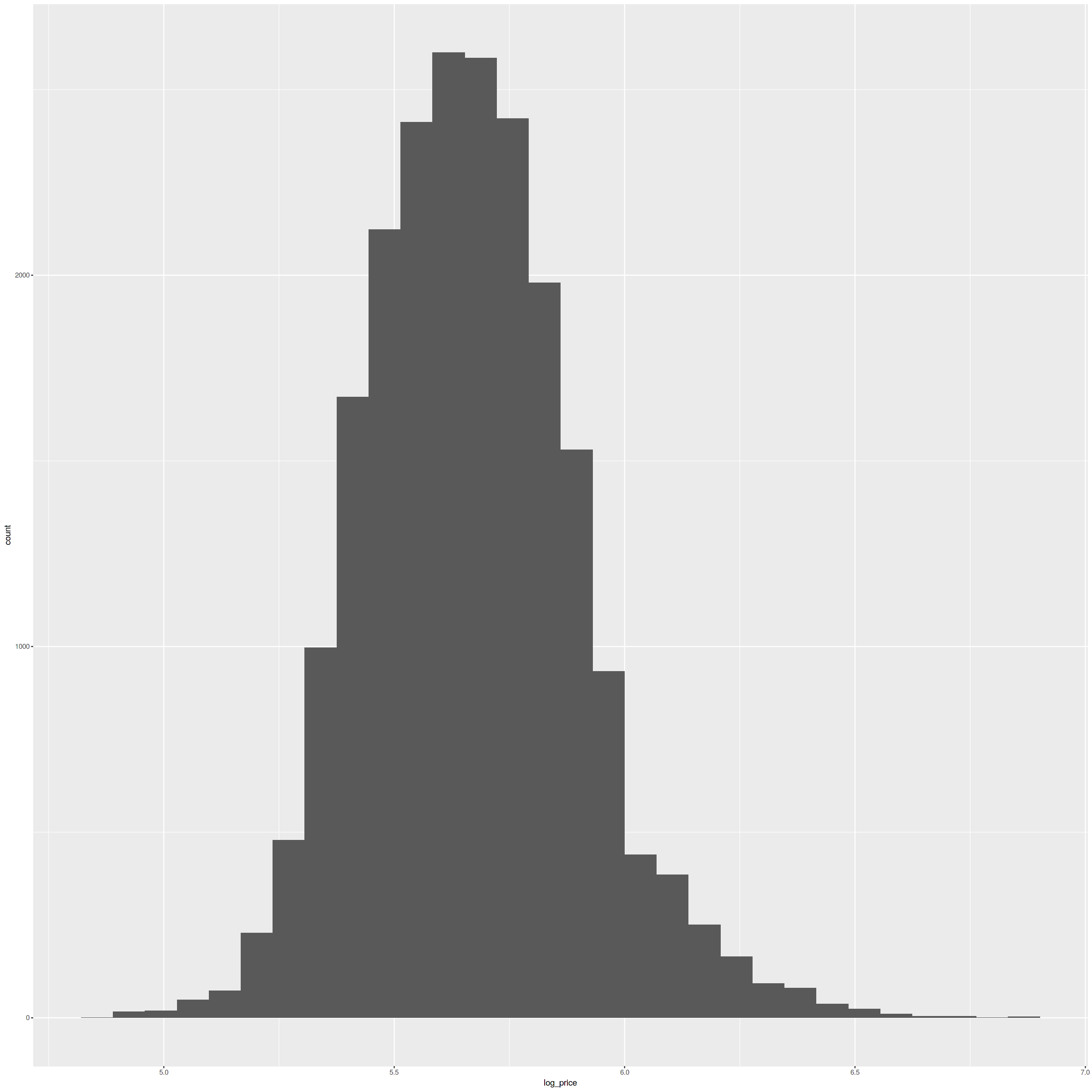
横軸が対数変換をした家の価格、縦軸がその価格の家の数です。先ほどよりわかりやすくなりましたね。
次に、今回のデータから数値で表される特徴のみをヒストグラム化して一覧表示させます。以下のコードを実行することで、複数グラフを一覧表示してた描画ができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
p1 <- ggplot(data, aes(x=price))+geom_histogram() p2 <- ggplot(data, aes(x=bedrooms))+geom_histogram() p3 <- ggplot(data, aes(x=bathrooms))+geom_histogram() p4 <- ggplot(data, aes(x=sqft_living))+geom_histogram() p5 <- ggplot(data, aes(x=sqft_lot))+geom_histogram() p6 <- ggplot(data, aes(x=floors))+geom_histogram() p7 <- ggplot(data, aes(x=waterfront))+geom_histogram() p8 <- ggplot(data, aes(x=view))+geom_histogram() p9 <- ggplot(data, aes(x=condition))+geom_histogram() p10 <- ggplot(data, aes(x=grade))+geom_histogram() p11 <- ggplot(data, aes(x=sqft_above))+geom_histogram() p12 <- ggplot(data, aes(x=sqft_basement))+geom_histogram() p13 <- ggplot(data, aes(x=yr_built))+geom_histogram() p14 <- ggplot(data, aes(x=yr_renovated))+geom_histogram() p15 <- ggplot(data, aes(x=zipcode))+geom_histogram() p16 <- ggplot(data, aes(x=lat))+geom_histogram() p17 <- ggplot(data, aes(x=sqft_living15))+geom_histogram() p18 <- ggplot(data, aes(x=sqft_lot15))+geom_histogram() # 複数グラフを並べて描画 gridExtra::grid.arrange(p1, p2, p3, p4, p5, p6, p7, p8, p9, p10, p11, p12, p13, p14, p15, p16, p17, p18) |
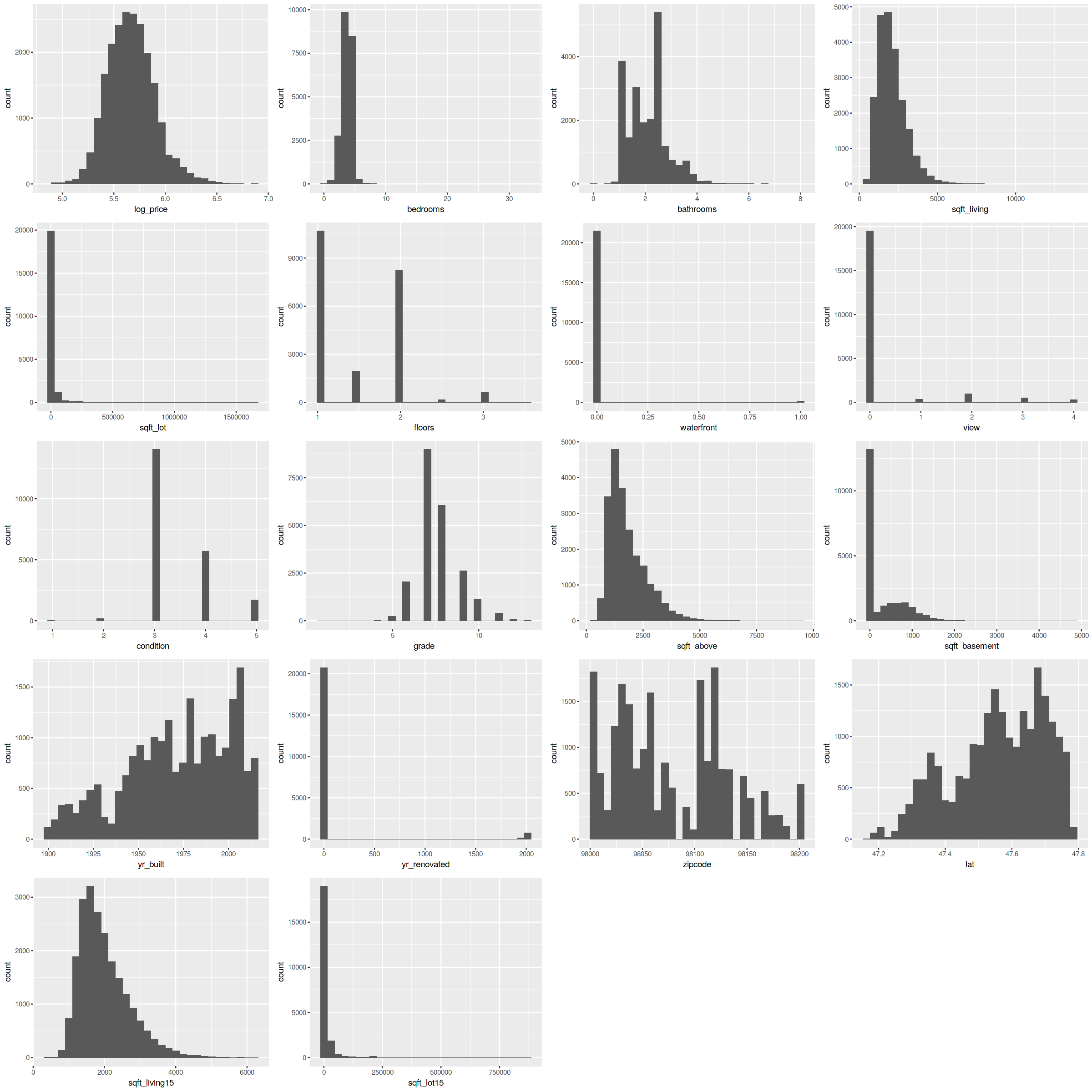
これで、データの概要として、各変数の分布をみることができました。この分布をじっくり見ることで、いろんなことがわかりそうです。
散布図・回帰直線の描画
次に、目的である「家の価格に大きい影響をもつ特徴の把握」のために、散布図とその回帰直線を描画してみます。散布図とは、2種類の項目を縦軸と横軸にとり、プロットにより作成される図です。2種類の項目の間に相関関係があるか否かの調査の役に立ちます。また、散布図に回帰直線を描くことで、予測もできます。回帰直線とは、散布図における分布の傾向をみるときに用いられる直線のことです。
最小二乗法と呼ばれる算術によって、求められます。
まずは、“価格”と“寝室の数”との関係を見てみましょう。
以下のコードを実行することで、散布図、および回帰直線の描画ができます。
|
1 2 3 4 5 6 |
# 価格と他の変数の関係をみたい options(scipen=999) options(repr.plot.width=20, repr.plot.height=20, align="center") p2 <- ggplot(data, aes(x=bedrooms, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p2 |
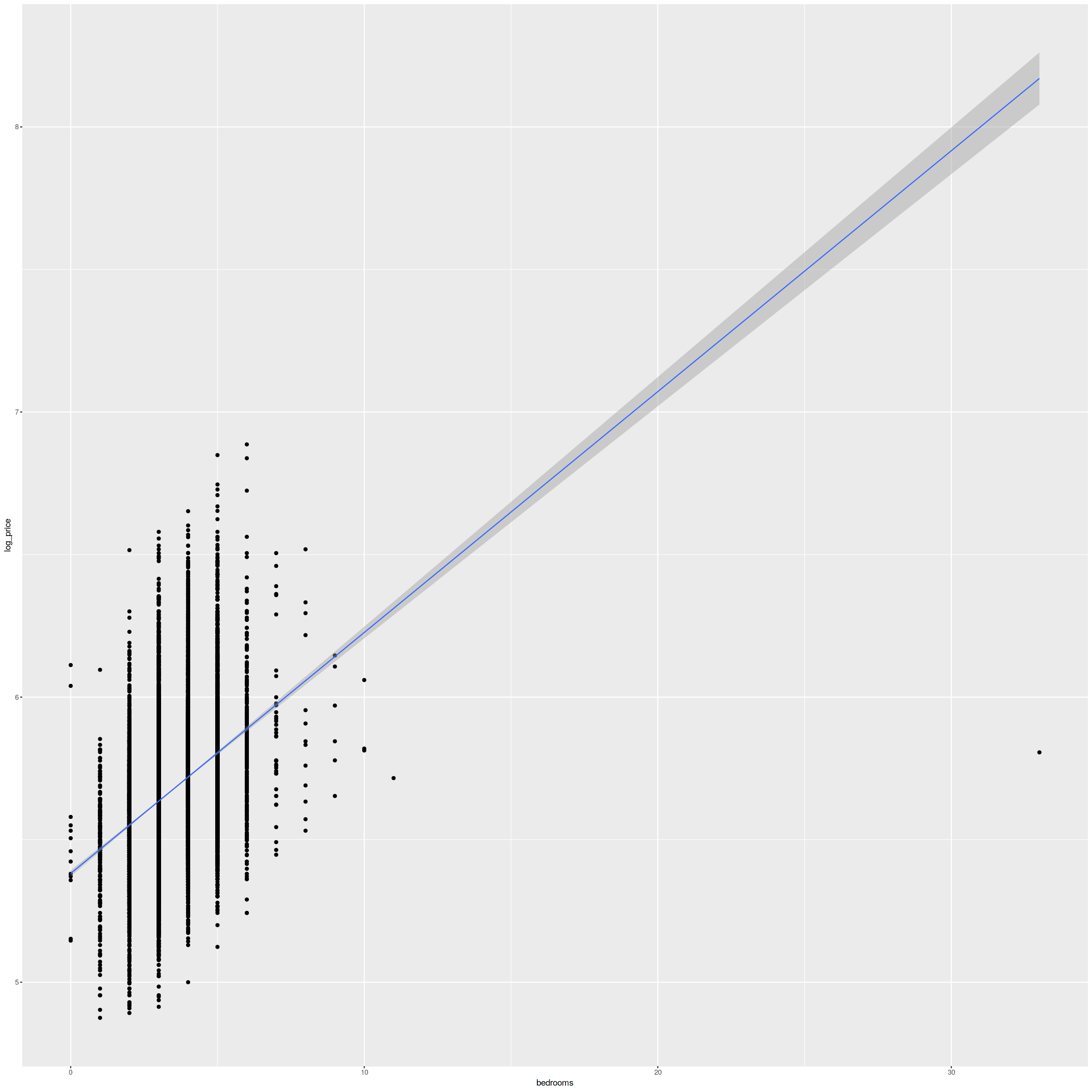
横軸が寝室の数（bedrooms）、縦軸が対数変換した家の価格です。散布図および回帰直線をみると、寝室の数の増大に対して、価格も増大していることがわかりますね。これが正の相関がある状態です。
同じ要領で、価格と他の変数との関係も一覧表示して見てみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
p2 <- ggplot(data, aes(x=bedrooms, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p3 <- ggplot(data, aes(x=bathrooms, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) # 値段と他の変数の関係をみたい。散布図と options(scipen=999) options(repr.plot.width=20, repr.plot.height=20, align="center") p2 <- ggplot(data, aes(x=bedrooms, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p3 <- ggplot(data, aes(x=bathrooms, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p4 <- ggplot(data, aes(x=sqft_living, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p5 <- ggplot(data, aes(x=sqft_lot, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p6 <- ggplot(data, aes(x=floors, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p7 <- ggplot(data, aes(x=waterfront, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p8 <- ggplot(data, aes(x=view, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p9 <- ggplot(data, aes(x=condition, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p10 <- ggplot(data, aes(x=grade, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p11 <- ggplot(data, aes(x=sqft_above, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p12 <- ggplot(data, aes(x=sqft_basement, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p13 <- ggplot(data, aes(x=yr_built, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p14 <- ggplot(data, aes(x=yr_renovated, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p15 <- ggplot(data, aes(x=zipcode, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p16 <- ggplot(data, aes(x=lat, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p17 <- ggplot(data, aes(x=sqft_living15, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) p18 <- ggplot(data, aes(x=sqft_lot15, y=log_price))+geom_point()+stat_smooth(method="lm", se=T, size=0.5) gridExtra::grid.arrange(p2, p3, p4, p5, p6, p7, p8, p9, p10, p11, p12, p13, p14, p15, p16, p17, p18) |
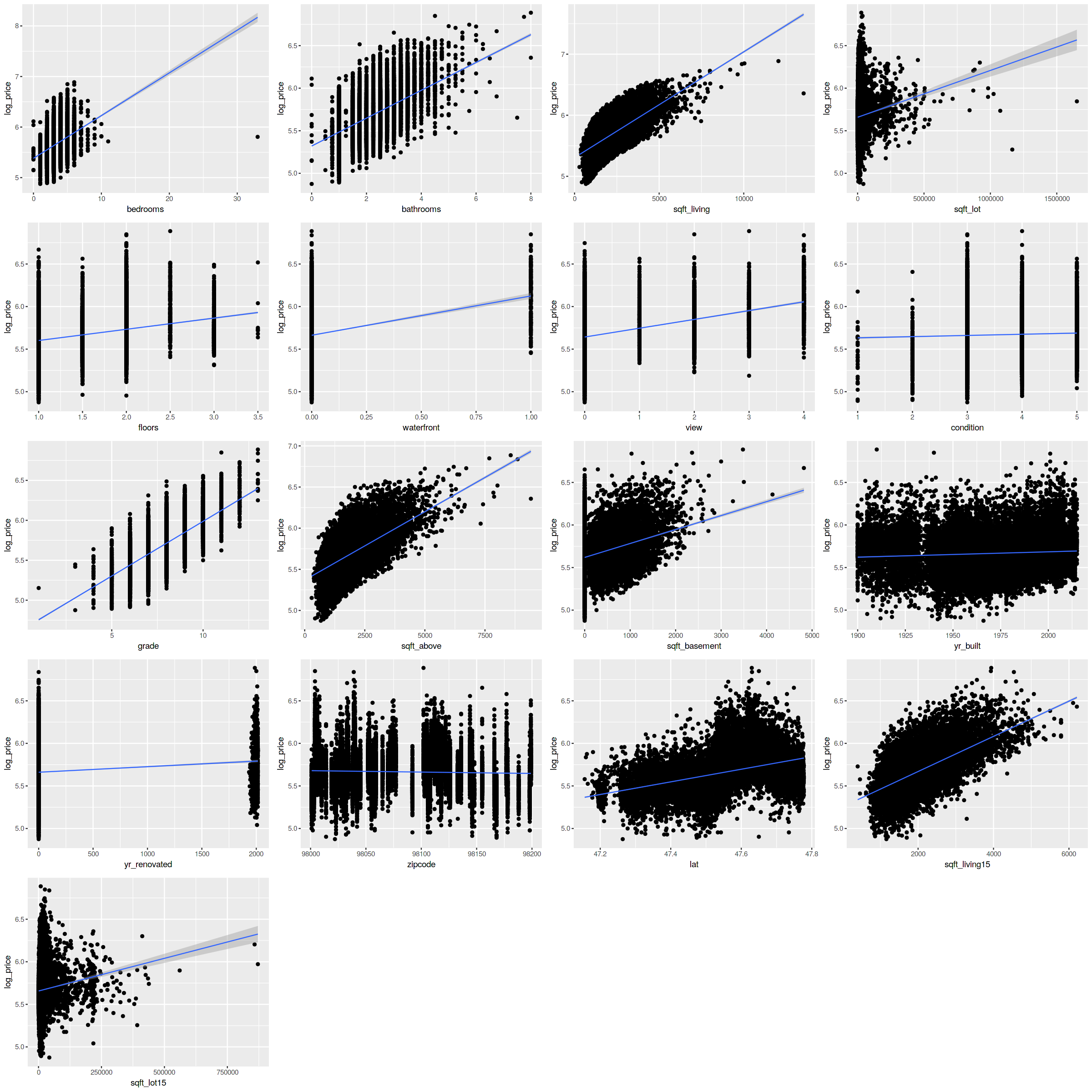価格は、ほどんどの変数と正の相関がありそうということがわかりました。
やはり、どんな要素でも多かったり、大きかったりすると価格が高いということがグラフからもわかります。
ヒートマップの描画
次に、これら変数間の相関を比較しやすくするために、各変数間の相関係数をヒートマップにより、見てみましょう。ヒートマップは、行列の個々の値を色や濃淡として表現した可視化グラフの一種であり、色により相関係数を比較できます。
以下のコードを実行することで、ヒートマップの描画ができます。ヒートマップ上同じ色付けとなったものの間でも関連性を比較できるように、各セル内に相関係数の値も表示させます。
|
1 2 3 4 |
col <- colorRampPalette(c("#BB4444", "#EE9988", "#FFFFFF", "#77AADD", "#4477AA")) corr<-cor(data[, 4:22]) corrplot(corr, method="shade", shade.col=NA, tl.col="black", tl.srt=45, col=col(200), addCoef.col="black", addcolorlabel="no", order="AOE") |
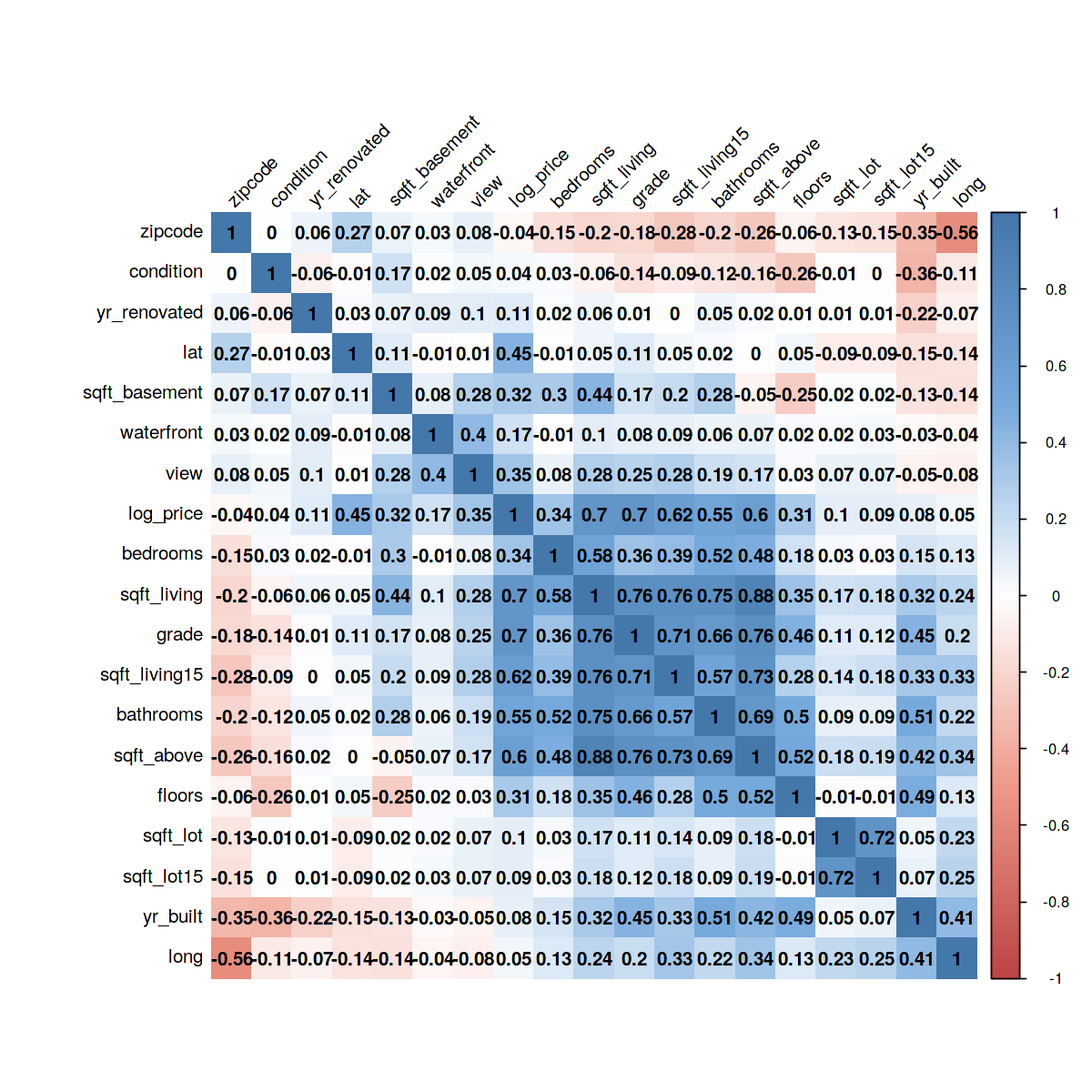
上記のヒートマップから、価格（log_price）は次の特徴と比較的高い相関があるといえます。
- 見た目（view）
- 寝室の数（bedroom）
- 水辺に立地しているか否か（waterfront）
- リビングの平米（sqft_living）
つまりは、これらが価格に与える影響は大きいということです。
水辺あたりに、広いリビング、大量の寝室、そして、とても見た目が良い、そんな家に住む夢はまだまだ先のようですね・・・
まとめ
本記事では、Rによるデータ分析について超入門的な内容を紹介しました。特にデータ全体の概要を読み解くためにいくつかの手法によりデータを可視化させました。その結果「家の価格に大きい影響をもつ特徴」とした4つの特徴を挙げる事ができました。
たとえばcsvなど、データが羅列された形式のまま、そこから人が目視で特徴を把握することは困難です。特に、データが大きいほど現実的でなくなります。このような場合にRなどを利用してデータ分析、可視化することでデータがその中にもつ特徴を容易に読み取れる事ができます。是非、利用してみてはどうでしょうか？
最後まで読んでいただきありがとうございました。
参照
- House Sales in King County, USA | Kaggle(https://www.kaggle.com/harlfoxem/housesalesprediction) より取得(2019/09/10)
