機械学習のハイパーパラメータ探索 : ベイズ最適化の活用

こんにちは、岡崎です。
この記事は TECHSCORE Advent Calendar 2016 の 20 日目の記事です。

先日、IBISML2016(第19回情報論的学習理論ワークショップ) のチュートリアルに参加しました。
その中で「ベイズ最適化による機械学習のハイパーパラメータチューニング」という内容が面白かったので紹介します*1。

ハイパーパラメータ・チューニング

機械学習モデルの学習においては、良いモデルを作るためにハイパーパラメータ(外部から与えるモデルのパラメータ)のチューニングが必須です。

目的の精度や汎化性能をもとめて、モデルの学習を繰り返し最適なハイパーパラメータを探索するのですが、選択するアルゴリズムやデータ量、計算環境によっては一回の試行が数時間に及ぶこともあり、効率よく探索することが大事になります*2。

従来よりハイパーパラメータのチューニングでは「グリッドサーチ」という手法がよく用いられています*3。
グリッドサーチはその名の通り、取りうる範囲のハイパーパラメータを全て探索し、その中から最適なパラメータを選び出す手法です。
シンプルで分かりやすいのですが、ハイパーパラメータの種類が増えると組み合わせ数が爆発してしまい、時間やリソース占有などが問題となってきます。

機械学習はロジックを選択・構築するだけがスコープではありません。
寧ろ、コストと苦労をかけて構築したモデルを最大限活用していく上では、モデルのアップデートなどの運用面がメインのタスクになり、こういった問題はより大切に、より切実になってきますね。

今回紹介するのは、グリッドサーチに代わってベイズ最適化を用いるとより効率的に最適なハイパーパラメータを探索することができるよ、という話で機械学習サービスの運用においても力を発揮するものです。

ベイズ最適化によるハイパーパラメータ最適化

この記事では理論的な背景については深く触れず、シンプルなアルゴリズムの実装を通してベイズ最適化の活用イメージを紹介します。

理論的背景について詳細を知りたい方は*1を参考にしてくださいね。

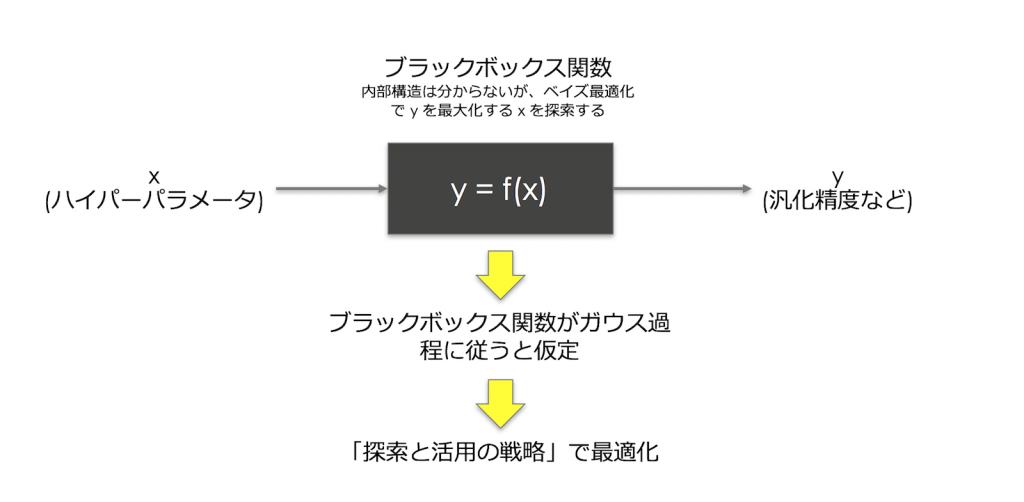
講義で紹介されていたベイズ最適化アルゴリズムは、信頼区間戦略(Gaussian Processs Upper Confidence Bound (GP-UCB) アルゴリズム)[Srinivas+, 2010]で、

入力(ハイパーパラメータ)と出力(最大化したいもの、精度など)の関係をブラックボックス関数とみなし
それをガウス過程(Gaussian Process)に従うと仮定して
「探索と活用の戦略」(Upper Confidence Bound)で最適化し y を最大化する x を探索する

というものです。

アルゴリズム

今回は、この GP-UCB アルゴリズムを実装しました。

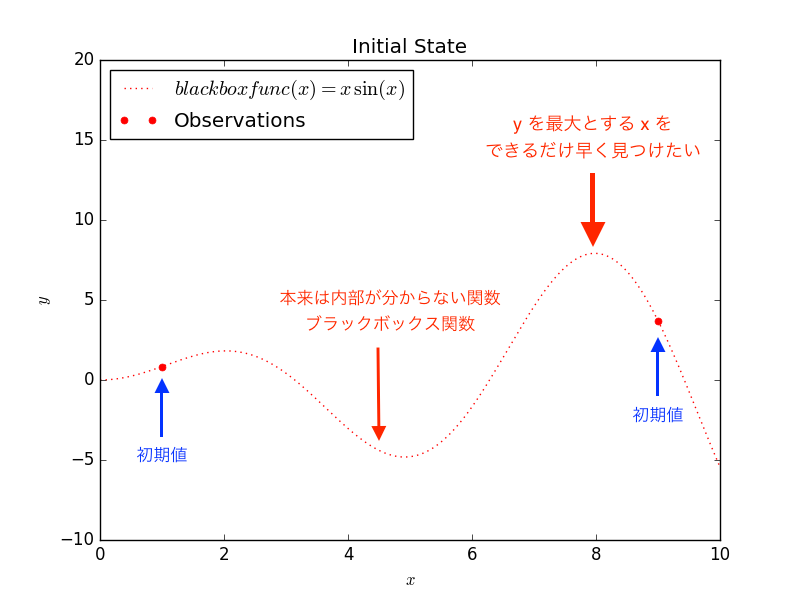
x はハイパーパラメータで、y がモデル学習結果（汎化精度や誤差等）と置き換えて下さい。
x は 0 から 10 の間を 0.01 刻みで取りうるとし、この中で「y を最大化する x をできるだけ少ない探索で求める」というのがアルゴリズムの目的です。
ブラックボックス関数は y = x sin(x) としています（もちろん本来は内部構造がわからないものですが、例題として講義と同じものにします）。

もし、従来手法のグリッドサーチで探索した場合、取りうる範囲の全ての x を探索するため、1000 回の試行を行います。

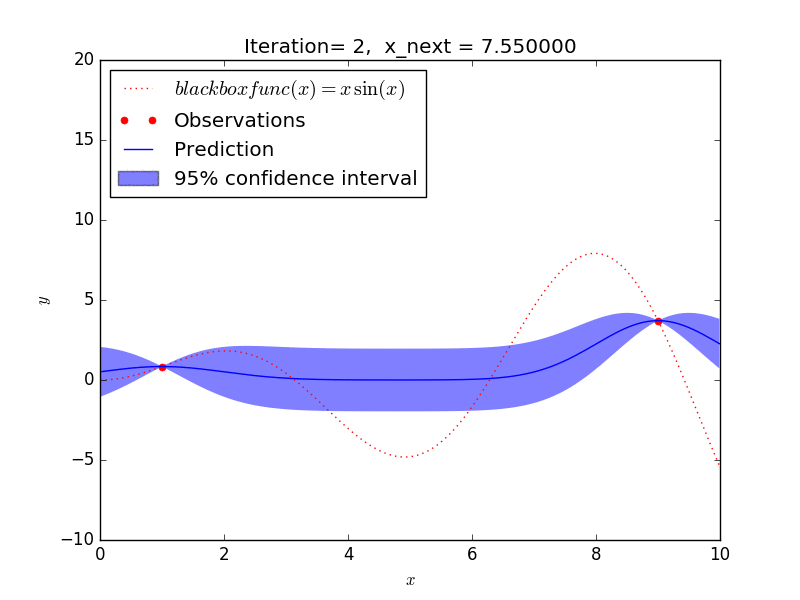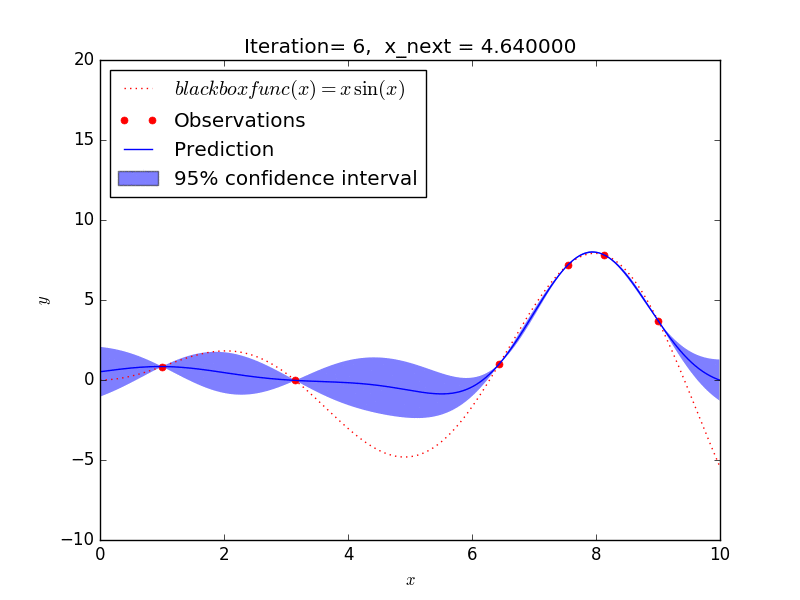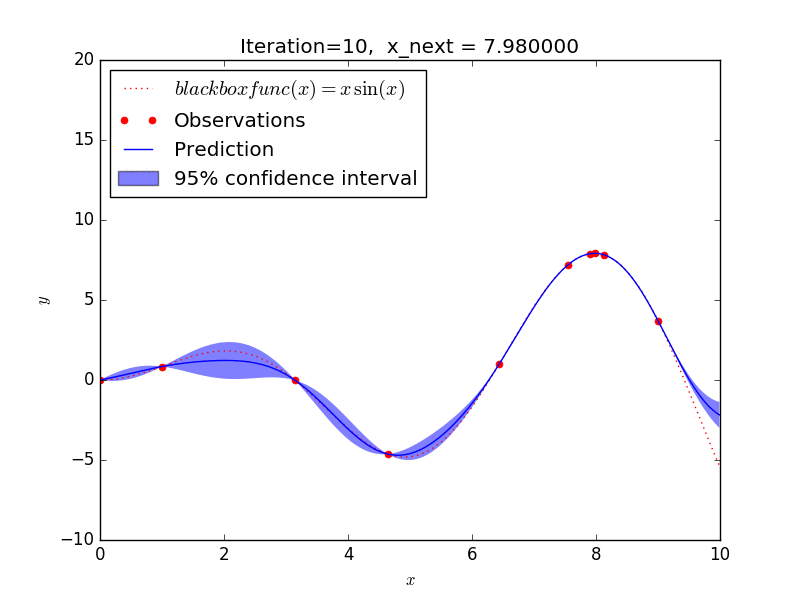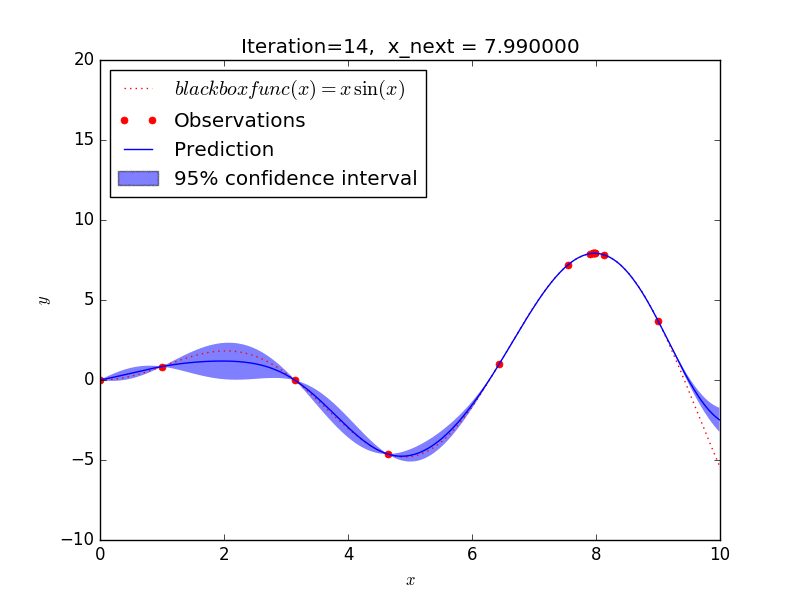
これを GP-UCB アルゴリズムで探索した場合、大体 10 回程度の探索で y が最大となる x を求めることができました。

探索の仕方を見ると、

探索があまりされていない範囲(探索)と
既に分かっている最大値に近い範囲(活用)を

バランスよく選択しながら探索を進めることが見て取れ、強化学習のようなアルゴリズムになっていますね。

まとめ

今日紹介したようなシンプルな例題では非常に効率よく最適値までたどり着くことができています。

例では分かりやすさを優先し、１種類のパラメータのみを探索したのでそれほどインパクトはないかもしれません。
しかし、もし 2 種類のパラメータがそれぞれ 1000 の範囲を取りうる場合、グリッドサーチでは 1000x1000 回の試行が必要になります。
3 種類のパラメータがそれぞれ 1000 の範囲を取りうる場合、1000x1000x1000 回の試行となり、最早現実的な試行回数にならないことがわかると思います。
探索するパラメータ次元数・取りうる範囲が増えるほど、ベイズ最適化は力を発揮するでしょう。

しかし、現実の問題にこのアルゴリズムを適用して即座にハイパーパラメータ・チューニングの悩みから解放される、という訳にはいかないと思います。

なぜなら GP-UCB アルゴリズムにもチューニングすべきハイパーパラメータ（*4）があり、これらを最適化したい機械学習モデルのハイパーパラメータ分布にフィットさせる工夫は要るでしょう。

機械学習のハイパーパラメータをチューニングするためのベイズ最適化アルゴリズム、のハイパーパラメータのチューニング・・・と少しお寒い感じがしてきますが(笑) ...
ただ、グリッドサーチでたくさんの次元のハイパーパラメータを直接相手にする必要がなくなることは期待できると思います。

ベイズ最適化は機械学習のハイパーパラメータチューニングだけでなく、様々な課題に適用することができます。
複数のパラメータを自動的にチューニングしながら、少しずつ最適なところを探していく・・・・様々なところに応用できそうですね。

コード

最後に実装コードを載せます。

アルゴリズムが理解できれば特に実装上注意するところはないと思いますが、私は獲得関数による次の x の選択のところで

a(x_next) = argmax μ(x) + √β σ(x) --> 獲得関数が最大を与えるときの x を次の x とする
を
x_next = argmax μ(x) + √β σ(x) --> 獲得関数の最大値を次の x とする
と読み間違えてしまい、しばらく悩みました。
こういった数式の読み違いミスはアルゴリズム実装には付きものですね・・・。

#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
ベイズ最適化(GP-UCB アルゴリズム)による探索.

環境
  Python 2.7.12
  scikit-learn==0.18.1
  matplotlib==1.5.3
  numpy==1.11.2
"""
import sys
import os
import matplotlib.pyplot as plt
import numpy as np
from sklearn.gaussian_process import GaussianProcessRegressor


def blackbox_func(x):
    """
    ブラックボックス関数（例題なので x sin(x) としています）
    --> 本来はモデル学習
        ex) y = svm(学習データ, x(ハイパーパラメータ)) の結果など最大化したい値を返す.
    """
    return x * np.sin(x)


def acq_ucb(mean, sig, beta=3):
    """
    獲得関数 (Upper Confidence Bound)
    $ x_t = argmax\ \mu_{t-1} + \sqrt{\beta_t} \sigma_{t-1}(x) $
    """
    return np.argmax(mean + sig * np.sqrt(beta))


def plot(x, y, X, y_pred, sigma, title=""):

    fig = plt.figure()
    plt.plot(x, blackbox_func(x), 'r:', label=u'$blackbox func(x) = x\,\sin(x)$')
    plt.plot(X, y, 'r.', markersize=10, label=u'Observations')
    plt.plot(x, y_pred, 'b-', label=u'Prediction')
    plt.fill(np.concatenate([x, x[::-1]]),
             np.concatenate([y_pred - 1.96 * sigma,(y_pred + 1.96 * sigma)[::-1]]),
             alpha=.5, fc='b', ec='None', label='95% confidence interval')
    plt.xlabel('$x$')
    plt.ylabel('$y$')
    plt.ylim(-10, 20)
    plt.title(title)
    plt.legend(loc='upper left')
    plt.savefig('fig%02d.png' % (i))



   
# アプリケーションエントリポイント
if __name__ == '__main__':
    
    # パラメータの取りうる範囲
    x_grid = np.atleast_2d(np.linspace(0, 10, 1001)[:1000]).T
    
    # 初期値として x=1, 9 の 2 点の探索をしておく.
    X = np.atleast_2d([1., 9.]).T
    y = blackbox_func(X).ravel()

    
    # Gaussian Processs Upper Confidence Bound (GP-UCB)アルゴリズム
    # --> 収束するまで繰り返す(収束条件などチューニングポイント)
    n_iteration = 13
    for i in range(n_iteration):
    
        # 既に分かっている値でガウス過程フィッティング
        # --> カーネル関数やパラメータはデフォルトにしています(チューニングポイント)
        gp = GaussianProcessRegressor()
        gp.fit(X, y)
        
        # 事後分布が求まる
        posterior_mean, posterior_sig = gp.predict(x_grid, return_std=True)
        
        # 目的関数を最大化する x を次のパラメータとして選択する
        # --> βを大きくすると探索重視(初期は大きくし探索重視しイテレーションに同期して減衰させ活用を重視させるなど、チューニングポイント)
        idx = acq_ucb(posterior_mean, posterior_sig, beta=100.0)
        x_next = x_grid[idx]
    
        plot(x_grid, y, X, posterior_mean, posterior_sig, title='Iteration=%2d,  x_next = %f'%(i+2, x_next))
    
        # 更新
        X = np.atleast_2d([np.r_[X[:, 0], x_next]]).T
        y = np.r_[y, blackbox_func(x_next)]
        
    
    print "Max x=%f" % (x_next)

#!/usr/bin/env python

# -*- coding: utf-8 -*-

"""

ベイズ最適化(GP-UCB アルゴリズム)による探索.

環境

Python 2.7.12

scikit-learn==0.18.1

matplotlib==1.5.3

numpy==1.11.2

"""

import sys

import os

import matplotlib.pyplot as plt

import numpy as np

from sklearn.gaussian_process import GaussianProcessRegressor

def blackbox_func(x):

"""

ブラックボックス関数（例題なので x sin(x) としています）

--> 本来はモデル学習

ex) y = svm(学習データ, x(ハイパーパラメータ)) の結果など最大化したい値を返す.

"""

return x * np.sin(x)

def acq_ucb(mean, sig, beta=3):

"""

獲得関数 (Upper Confidence Bound)

$ x_t = argmax\ \mu_{t-1} + \sqrt{\beta_t} \sigma_{t-1}(x) $

"""

return np.argmax(mean + sig * np.sqrt(beta))

def plot(x, y, X, y_pred, sigma, title=""):

fig = plt.figure()

plt.plot(x, blackbox_func(x), 'r:', label=u'$blackbox func(x) = x\,\sin(x)$')

plt.plot(X, y, 'r.', markersize=10, label=u'Observations')

plt.plot(x, y_pred, 'b-', label=u'Prediction')

plt.fill(np.concatenate([x, x[::-1]]),

np.concatenate([y_pred - 1.96 * sigma,(y_pred + 1.96 * sigma)[::-1]]),

alpha=.5, fc='b', ec='None', label='95% confidence interval')

plt.xlabel('$x$')

plt.ylabel('$y$')

plt.ylim(-10, 20)

plt.title(title)

plt.legend(loc='upper left')

plt.savefig('fig%02d.png' % (i))

# アプリケーションエントリポイント

if __name__ == '__main__':

# パラメータの取りうる範囲

x_grid = np.atleast_2d(np.linspace(0, 10, 1001)[:1000]).T

# 初期値として x=1, 9 の 2 点の探索をしておく.

X = np.atleast_2d([1., 9.]).T

y = blackbox_func(X).ravel()

# Gaussian Processs Upper Confidence Bound (GP-UCB)アルゴリズム

# --> 収束するまで繰り返す(収束条件などチューニングポイント)

n_iteration = 13

for i in range(n_iteration):

# 既に分かっている値でガウス過程フィッティング

# --> カーネル関数やパラメータはデフォルトにしています(チューニングポイント)

gp = GaussianProcessRegressor()

gp.fit(X, y)

# 事後分布が求まる

posterior_mean, posterior_sig = gp.predict(x_grid, return_std=True)

# 目的関数を最大化する x を次のパラメータとして選択する

# --> βを大きくすると探索重視(初期は大きくし探索重視しイテレーションに同期して減衰させ活用を重視させるなど、チューニングポイント)

idx = acq_ucb(posterior_mean, posterior_sig, beta=100.0)

x_next = x_grid[idx]

plot(x_grid, y, X, posterior_mean, posterior_sig, title='Iteration=%2d, x_next = %f'%(i+2, x_next))

# 更新

X = np.atleast_2d([np.r_[X[:, 0], x_next]]).T

y = np.r_[y, blackbox_func(x_next)]

print "Max x=%f" % (x_next)

参照

チュートリアル講義はこちらで公開されている内容と重なるところも多いですので是非参考にして下さい.
特に DeepLearning などは一回の学習が数時間、場合によっては数日かかることも珍しくありません
ランダムにパラメータを振って探索するというのも立派な探索方法の一つです。DeepLearning ではグリッドサーチよりもランダムサンプリングの方が良いことが報告されています。
今回はわかりやすさを優先したため、ライブラリのデフォルト値を用い、探索戦略を UCB のみに限定しています。恐らく、探索と活用のバランスを決める係数 β の選び方やカーネル関数の種類で局所最適に陥ったりもするでしょう。

最後に

賢く探索、賢く最適化は怠け者の味方ということで、これらは猫の好物だと思います。

かわいいベッキー