こんにちは。一松です。
開発新卒に捧ぐシリーズ第3回の今回は、アルゴリズムとあわせておさえておきたいデータ構造についてお話します。データ構造を理解することで、プログラムの目的に沿って適切な構造を選べるようになるので、動くだけのコードからの質の高いコードを書くステップアップとして読んでみてください。
データ構造とは
そもそもデータ構造とは何でしょうか。データ構造は、データをコンピュータの中で扱う際にデータを格納する一定の形式のことです。例えば、プログラミングを経験したことがある人は配列やリストを使ったことがあると思います。じつは、それらもデータ構造の一種です。プログラムを書く際にはどのような処理を行うのかを事前に考え、その処理にとって最適なデータ構造を選択する必要があります。そのためにも、それぞれのデータ構造の特徴(長所、短所)を知っておくことが大切です。特徴を考える要素として、データに対してどんな操作ができるのか、計算量はどれくらいなのか、があります。計算量ってなんだ?という人は、アルゴリズムに関する記事の中で説明しているので、参考にしてください。【開発新卒に捧ぐ、基本のアルゴリズムと計算量】
代表的なデータ構造
今回の記事ではBag、Sequence、Tree、Mapの4つの構造(考え方)と、その実装(具体的な実現方法)をご紹介します。
Bag
Bagは、データを格納した順序付けはなく、重複したデータを格納することができます。また、Bagの構造の中でもデータの重複を許さないものをSetといいます。Bagは重複データを扱えるため、延べ人数を記録するようなデータにむいているのに対し、Setは重複を除けるためユニークな人数を記録するようなデータにむいています。
実装は、後で詳しく紹介する配列や木構造をつかって実現することができます。したがって計算量も実装方法によって異なるので注意が必要です。
Sequence
データが順に並んでいるような構造をSequenceといいます。データの格納順をインデックスとして記録できるため、特定の要素を指定して参照したり、取り出したりといった操作が可能です。Sequenceの実装方法として主に配列とリストがあります。それぞれの違いを次の説明でおさえておきましょう。
配列(Array)
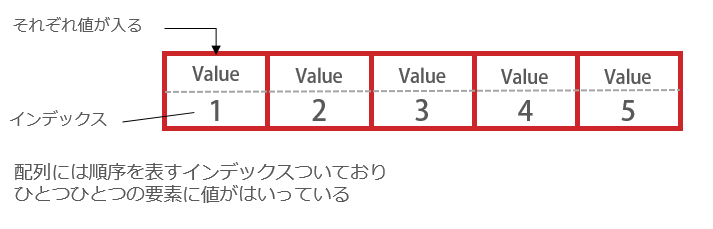
同じ型のデータをインデックスをもとに格納していきます。この時の型とは数値や文字列といった個々のデータに対する型のことです。要素数をあらかじめ決めてからデータを格納するため、領域の拡張ができません。データを追加するには予め余分に領域を確保しておくか、より大きい配列を新しく作成し現在の内容をコピーして移す必要があります。データにアクセスする際の計算量はインデックスをもとに直接指定の要素アクセスできるのでO(1)、データ検索はインデックスを辿る必要があるのでO(n)です。ただしデータ追加は、配列ははじめに配列の要素数を決めてしまうためデータの追加ができません。
■データアクセス時の計算量
先頭アクセスO(1)
ランダムアクセスO(1)
末尾アクセスO(1)
■データ追加時の計算量
O(1) ※配列をコピーして移す場合はO(n)
■検索
O(n)
リスト(List)
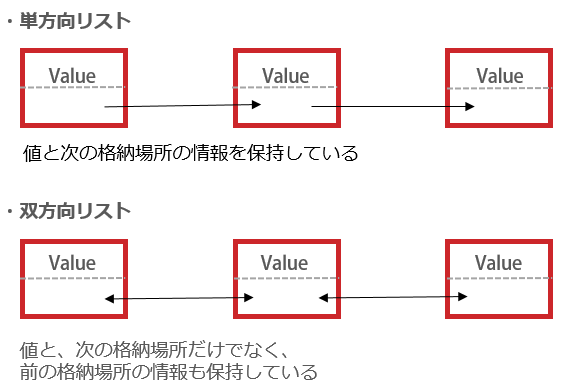
前述の配列はインデックスをもとにデータを要素に格納していましたが、リストでは各要素に次の要素のリンクを保持させます。最後の要素は次の要素のリンクを持たせないことで表現します。リストには次の要素をどのように保持しているかによって2種類あり、次の要素へのリンクのみを保持していて、一定の順序でしかアクセスできないものを単方向リスト、前後のリンクを保持しているものを双方向リストと呼びます。
リストはあらかじめ要素数を決めておく必要がなく、データの増減に合わせて調整することができるので、データを記録するためのメモリ効率が良いというメリットがあります。しかしデータを取り出す際には最初の要素から順にリンクを辿っていかなければならないため、計算量はO(n)と要素数にあわせて増えてしまいます。追加する際は直接挿入したい場所へ追加できるので計算量はO(1)です。
単方向リストの時
■データアクセス時の計算量
先頭アクセスO(1)
ランダムアクセスO(n)
末尾アクセスO(n)
■データ追加時の計算量
先頭への追加O(1)
任意の場所への追加O(1)
※ただし、追加する前に任意の場所へアクセスするのでO(n)かかります
末尾への追加O(n)
■検索
O(n)
Tree
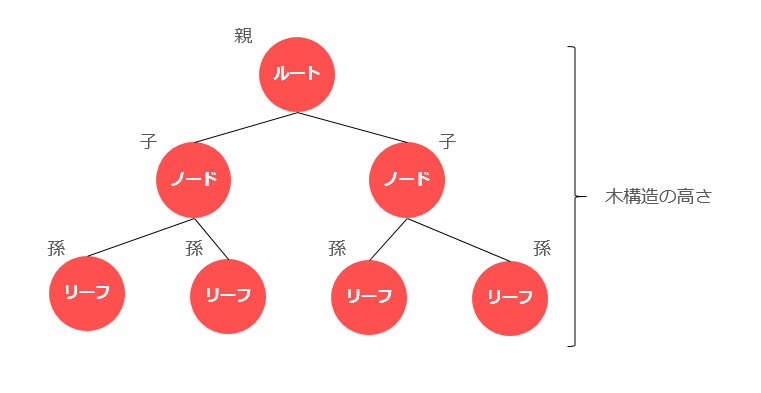
前述のデータ構造より複雑なデータ構造を実装できるのが木構造です。木構造は階層関係を表すことができます。階層関係の例としては会社の組織構造や、PCでフォルダを使ってファイルを管理するような構造です。これらのように概念の上下関係(親子関係)があるような関係を階層関係といいます。
木構造では、ひとつひとつの要素をノードといいます。親に当たるノードを持たないノードをルートといい、子にあたるノードを持たないノードをリーフといいます。また、それぞれのノードをつなぐ枝はエッジといいます。
二分探索木
木構造にも様々な種類がありますが、二分探索木を例に考えます。ルートノードの任意の値に対して、左のノードはルートノードよりも小さく、右のノードはルートノードよりも大きいという関係が成り立つように値を入れていきます。これを下の階層のノードでも繰り返します。一つ上のノードに対しての大小なので、データを取り出す際には必ずルートから順にノードを検索する必要があります。計算量は木構造の高さ(階層の数)に比例し、O(log n)となります。ただし、木構造の一方にノードが集中するして偏った構造になる場合O(log n)よりも遅いO(n)に近づいて遅くなる懸念があります。
■データアクセス時の計算量:O(log n)
■データ追加時の計算量:O(log n)
Map
Mapの最大の特徴はひとつの要素内に、データの場所を表す「キー」と、データの「バリュー」を対応付けて格納することです。データの保管場所をキーとすることで、SequenceでもTreeでも実装することができます。
ハッシュ(Hash)
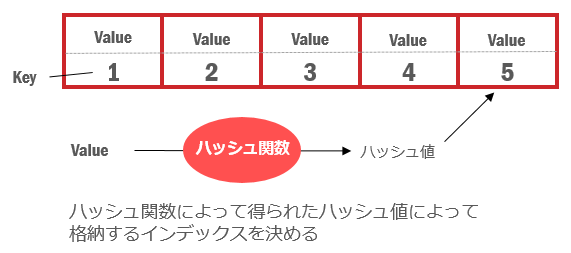
キーとの結びつけをハッシュ関数という計算式によって行います。まず、格納するデータからハッシュ関数を用いて、ハッシュ値という値を得ます。その値をキーとしてデータを格納する場所を決めます。しかし、別々のデータから計算したハッシュ値が等しくなってしまい、すでに利用されているキーの要素にデータを格納しようとしてしまうことがあります。これを衝突といいます。その際に、ハッシュ値を求め直して格納場所を移動させることをクローズドハッシュ法といいます。また、同じ要素の中でリスト構造を作りデータを追加していく方法をオープンハッシュ法といいます。下記の図では配列での実装を表しています。
■データアクセス時の計算量 : O(1)
■データ追加時の計算量 : O(1)
■検索 : O(1)
データ構造の特徴
今回紹介したデータ構造の特徴を表にまとめました。実装方法は紹介した以外にもたくさんありますので、是非調べてみてください。
※小さくて見にくい場合は画像をクリックして拡大表示して下さい。
おわりに
データ構造はその時々によってどれを用いるのが効率的なのか、最適な選択をすることが求められます。それができると同じ処理をもったコードでも、より処理が速く、よりメモリの使用量を抑えた、保守性の高い、質の高いコードを書くことにつながります。今回紹介したデータ構造以外にも、キュー、スタックなどたくさんの種類があるので、実際に皆さんがコードを書く際には、計算量やデータへのアクセス方法を確認しながら使ってみてください。