クラスタリングには様々な手法がありますが、目的、データの分布などに合わせて適切なものを選択します(1).
今は強力なツール、ライブラリが揃っていますので大体はそれでまかなえてしまいますし、様々な高度なアルゴリズムをすぐに使うことができます(2).
しかし、アルゴリズムによっては提供されていないこともありますので、実装ができると幅が広がります.
今回紹介する「混合ディリクレ分布」は運悪く、私のよく使う sckit-learn にないため、頑張って実装してみようと思います(私自身、アルゴリズムを実装からするのは久々です..).
混合ディリクレ分布
今回は、「足したら 1 になるデータ」の集合に対する分布表現・クラスタリング手法を考えてみました.
このようなデータには例えば、当社の顧客価値観モデル「Societas」があります.
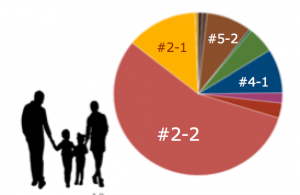
Societas では人の価値観を 12 の特性パターンの割合(所属確率)で表現します.具体的には例えばある人の価値観を、
[パターン 2-2 家庭的な真面目タイプ]:60%
[パターン 2-1 家族大好き悠々タイプ]:15%
[パターン 4-1 自分中心的なアクティブタイプ]:10%
[パターン 5-2 社交的な堅実ホームメーカータイプ]:10%
...
のように表現しますが、こういったデータに分布にあてはめる場合です.
例えば、上の例のソシエタスの割合からできる価値観イメージは「実用性を重視した、しっかり派」で、下図のようなパイチャートで表現したりします.
さて、このようなデータの分布モデルとしてはディリクレ分布があり、「サイコロの出目のでやすさ」の確率分布と言われ、いびつなサイコロで確率分布を表現するイメージになります(=ある面が出やすかったり出にくかったりしますが、出目の確率の和は 1 ).
今回はこのディリクレ分布を複数重ねあわせてデータ分布を表現します.
と言っても、実際には混合ガウス分布モデルのガウス分布をディリクレ分布に置き換えるだけです(3).
アルゴリズム
まず、データの分布を複数のディリクレ分布の重ね合わせで定式化します. α はディリクレ分布パラメータ、π は混合比と呼ばれる潜在変数、k は重ね合わせる分布の数です.
データの分布を表現できたらその尤度を最大化することで最適なパラメータを見つけることができますが、今回は混合ガウス分布と同様に EM アルゴリズムで見つけます.
異なるところは、M ステップでディガンマ関数の逆関数をニュートン法で解くところだけです.
- E ステップ
各混合要素の負担率を計算します. - M ステップ
現在の負担率を使って、パラメータ値を再計算します。
Q 関数は混合ガウス分布と同様ですが、ガウス分布をディリクレ分布と置き換えます。これは凸関数ですのでパラメータで偏微分し、最大化することで新しいパラメータと置き換えますが、
この時、ディガンマ関数の逆関数をニュートン法で解きます(4).
- E と M のステップを繰り返し、対数尤度が収束したときに得られる α、π が最適なパラメータ、潜在変数となります.
12345678910# E-M ステップ・イテレーションfor nstep in range(200):#### [E-step]E_step(K, X, alpha, pi, resp)#### [M-step]M_step(K, X, alpha, pi, resp)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def dirichlet_pdf(x, alpha): """ ディリクレ分布確率密度関数 """ return reduce(operator.mul, [x[d]**(alpha[d]-1.0) for d in range(len(alpha))]) * \ math.gamma(sum(alpha)) / \ reduce(operator.mul, [math.gamma(a) for a in alpha]) def E_step(K, X, alpha, pi, resp): """ データ xi が クラス C に所属する確率 responsibility [[estep.png]] """ for k in range(K): def f(x): return pi[k] * dirichlet_pdf(x, alpha[k]) / \ sum([pi[c] * dirichlet_pdf(x, alpha[c]) for c in range(K)]) resp[:, k] = np.apply_along_axis(f, 1, X) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
from scipy.special import polygamma digamma = lambda x: polygamma(0, x) trigamma = lambda x: polygamma(1, x) def inverse_digamma(y): """ ニュートン法によるディガンマ関数の逆関数解法 """ if y >= -2.22: x = np.exp(y) + 0.5 else: x = -1./(y+(-digamma(1))) while True: x_new = x - (digamma(x) - y) / trigamma(x) if abs(x_new - x) < 1.0e-8: break x = x_new return x_new def M_step(K, X, alpha, pi, resp): """ Q 関数の最大化 """ alpha_new = alpha # alpha update for k in range(K): for d in range(alpha.shape[1]): """ [[mstep_inv_digamma.png]] """ y = digamma(sum(alpha[k])) + (sum(resp[:, k] * np.log(X[:,d])) / sum(resp[:, k])) alpha_new[k][d] = inverse_digamma(y) # pi update for k in range(K): pi[k] = resp[:, k].sum() / X.shape[0] |
実際にやってみる
さて、この混合ディリクレ分布の EM アルゴリズムを実際に次の 3 次元データに適用してみます.
本当は Societas の分類数と同じ 12 次元でやってみたいのですが、各イテレーションでの分布を可視化したいですので 3 次元データにします.
データは足したら 1 ですので次のようなデータの集合になります.
|
1 2 3 4 |
X = np.array([ [ 0.5, 0.2, 0.3], [ 0.1, 0.4, 0.5], .... |
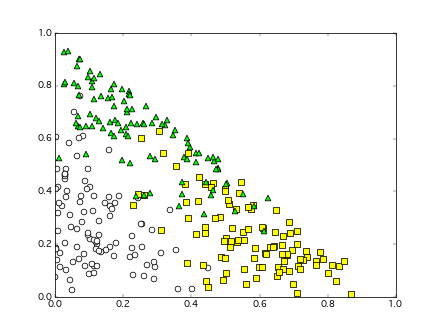
本来は 3 次元ですが、足したら 1 という制約がついていますので、2 次元上にマッピングできて、下図のような三角形領域内に分布します.
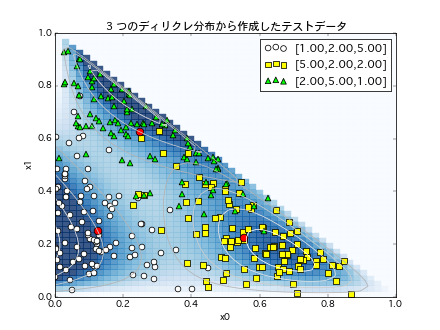
今回は 3 つのディリクレ分布から生成した、こんな感じのデータをテスト分布として、前述のアルゴリズムでこの分布パラメータが推定できるかどうかを試してみます.
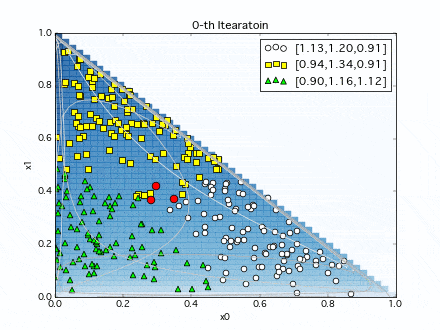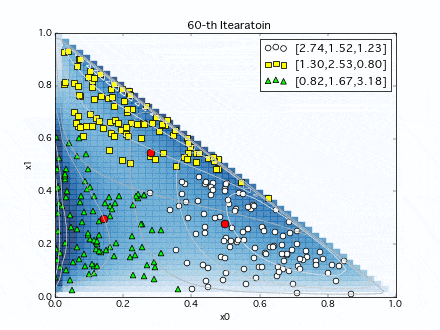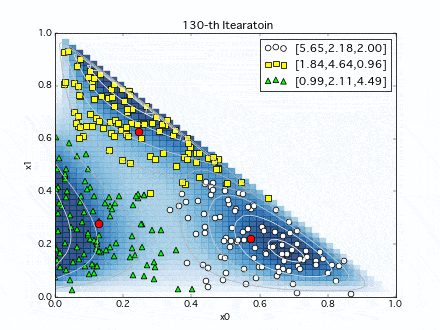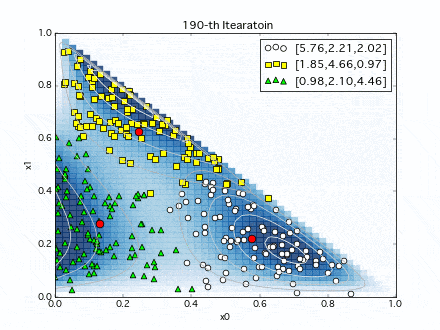
初期値は適当に設定して、各イテレーションでの推定分布の推移を見てみます.
赤点が推定分布の中心点(ディリクレ分布の期待値)ですが、イテレーションを繰り返すにつれ、テストデータに近づいてゆきます.
複数の分布の境界領域は微妙ですが(この領域の取り合いに分布モデルの個性がでそうですね.)、なんとなく(汗)元データの生成分布を推定できていそうです.
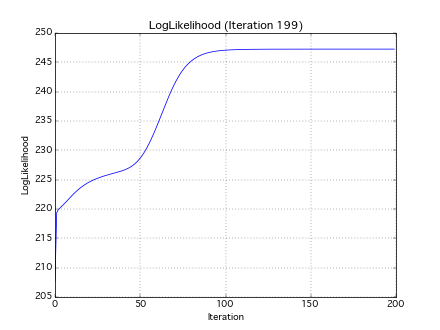
イテレーション毎の対数尤度の推移もプロットします.100 イテレーションくらいで収束に近づきます.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
def data_creation_k3_d3(a, N=300): """ 3 つのディリクレ分布からテストデータを作成 """ x0 = np.array([np.random.dirichlet(a[0]) for i in range(N/3)]) x1 = np.array([np.random.dirichlet(a[1]) for i in range(N/3)]) x2 = np.array([np.random.dirichlet(a[2]) for i in range(N/3)]) return np.vstack([x0, x1, x2]) N=300 # 正解データの分布 alpha_org = np.array([ [1., 2., 5.], [5., 3., 4.], [2., 5., 1.] ]) # データを作る X = data_creation_k3_d3(alpha_org, N) # ディリクレ分布パラメータ初期値を適当に設定(-> Kmeans の中心点を初期値にしてもよい) alpha = np.array([ [1.5, 1., 1.], [1., 1.5, 1.], [1., 1., 1.5]]) # 分布混合比率 : 一様分布で初期化 pi = np.ones(K)/K # 各ベクトルの各クラスへの所属確率 resp = np.zeros((N, K)) # E-M ステップ・イテレーション for nstep in range(200): ### # [E-step] E_step(K, X, alpha, pi, resp) ### # [M-step] M_step(K, X, alpha, pi, resp) |
終わりに
今回は簡単な実装とデータでやってみましたが、なんとなく混合分布モデルのイメージがつかめたと思います。
実際にはデータサイズや運用など諸々総合的に判断して(5)、実績のある機械学習ライブラリのアルゴリズムを採用することがほとんどでしょうが、実装すると理解が深まり適切なアルゴリズムの選択やパラメータ探索など役立つことも多いのではと思います.
分布の混合と潜在的変数はトピックモデルへと続く潜在的意味解析の入り口ですので、機会があればこの道を辿ってみたいと思います.
参考ですが、私は Emacs を使っており iimage-mode でよく関数のコメントに数式や手描きのポンチ絵の画像を差し込んだりします.後々、見なおしたりする際に、なかなか便利です.
|
1 2 3 4 5 |
def calc_log_likelihood(X, alpha, pi): """ [[likelihood.png]] <-- M-x iimage-mode で画像がインライン表示される. """ .... |
<脚注>
1) 例えば K-means や 混合ガウスモデルは、データ変数がカテゴリカルな場合には適切ではなかったりします(ユークリッド距離が適切ではないため)
2) 利点の反面、「ツールのできること > 自分のできること」、となってしまう傾向にあります.
3) パターン認識と機械学習 下 (ベイズ理論による統計的予測) 9.2.2章
4) Estimating a Dirichlet distribution. 数イテレーションで 10-14 桁精度になるそうです.
5) 最適なクラスタ数の探索や、尤度関数の発散する特異性に対する対策、等々