こんにちは、馬場です。
本番の講義終わりました!
あとは、この連載も完走します。今回は第7週、8週の内容です。
13. サポートベクターマシン
教師あり学習のオオトリは、SVM=サポートベクターマシンです。
SVM も ロジスティック回帰のように、分類をするアルゴリズムです。特徴は、「large margin classifier」と呼ばれるもので、
「境界線を引く場合、学習データより遠いところになるように引く」というものです。
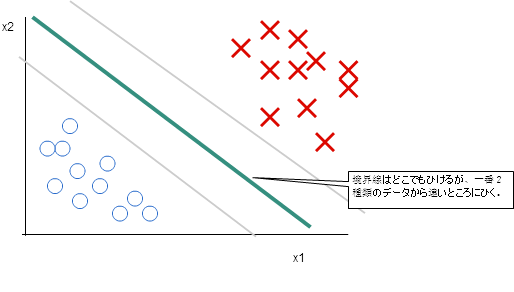
また、「カーネル」を変更することにより、境界線の形が変わります。linear kernel の場合、境界線の形が直線になりますが、Gaussian kernel の場合は、境界線が複雑な形になりますので、ロジスティック回帰で高バイアスが原因でうまく分類できない場合はおすすめです。ただし、Gaussian kernel を選択した場合入力ベクトルが学習データの次元のベクトルに変換しなおすので注意が必要です。いずれにしろ、SVMは複雑なので、liblinearやlibsvmなどの既存のライブラリを使うことをお勧めします。独自実装はするな、と。はい!
SVM の説明では、いままでモデルの関数から考えていたところ、ロジスティック回帰の尤度関数から新しい尤度関数を示していて、
面白いと感じました。
14. クラスタリング
さて、前回までで教師あり学習は一旦終了。今回から、教師なし学習です。教師あり学習はたくさんの「条件と答え」のデータを学習してモデルをつくり、新しい「条件」だけが与えられたときに「答え」を予測するものでした。対して、教師なし学習では「答え」はありません。では、何を学習するのか、というとデータの「構造」を学習するのです。
例えば、こんなデータの集合があったとします。
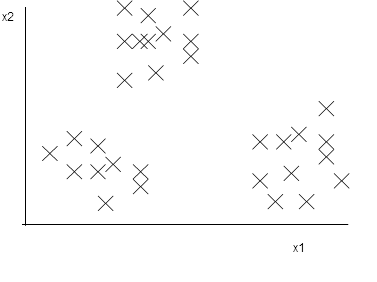
なんとなく、まとまったグループが3つあるように見えますね。このようなデータのまとまりという「構造」を見つけることを「クラスタリング」とよび、教師なし学習の代表的なものです。そして、最初の教師なし学習のアルゴリズムもクラスタリングのアルゴリズムです。
今回紹介するアルゴリズムK-meansはクラスタリングのアルゴリズムです。以下のようにクラスタを見つけ出します。
- クラスタの数を決める=k個。
- ランダムにk個の点をとる。これを各クラスタの中心にする。
- 一番近い点= そのクラスタに属する、とする。
- クラスタに属する点の平均をあらたにクラスタの中心とする
- 中心が移動しなくなる(あるいは回数を決めて)まで3.4 を繰り返す
K-meansでは、最初の中心の点の取り方によって、できるクラスタが異なります。もし標本数よりクラスタ数の方が小さければ、標本の中から最初の中心を選びましょう。また、K-meansでは各標本と属するクラスタの中心との距離の和を最小化するモデルが良いとされています。最初にとる中心の点によってかわりますので、何回か試行して良いものを採用しましよう。
もう一つ。適切なクラスタリングの数がいくつか、というのも気になります。機械的に算出する場合は、やはりクラスタの中心との距離の和をクラスタ数ごとにプロットしていき、グラフがかくっと曲がる部分(講義ではグラフの「肘」といっていました)をクラスタ数として採用します。
ただ、現実の問題に適用する場合、クラスタ数はむしろモデルでどのような構造を解明したいか、に依存します。例えば、体重と身長のデータをクラスタリングして、製造するTシャツのサイズを決めるような問題です。データの分布は一様になるので、上記のようにグラフの「肘」の箇所でクラスタ数を決めることは難しいでしょう。また、実際はビジネス的に「このTシャツは3サイズ展開だ!」「このTシャツは5サイズ展開!」と決められることの方が多く、それに従いクラスタの数が決まります。
K-means、結構使います。アルゴリズムが簡単なので、実装が楽です。とはいうものの、あんまりスケールしないんですよね。そこが課題でしょうか。
15. 次元の削減
変数が多くなると、いろいろなアルゴリズムの計算量がぐっと増えます。変数同士に関係がある場合、情報量を減らさずにうまく変数=次元を削減できれば、計算量が減っていいですよね。その方法の一つが主成分分析です。
例えば、2つの変数のデータが以下のように分布しているとします。

グラフをみてわかるように、平面上に均等にデータが存在するわけではなく、直線状に存在するように見えます。
この場合、直線をとり、直線へ垂線をおろした足の部分を座標として取り直せば、変数の数が2つから1つに減らせます。
同じように、その変数空間上に各点との距離の総和が最も少なくなるような超平面を描き、その面への射影を新たなデータとして利用するような操作をします。このような超平面をみつけるのが主成分分析です。ちなみに、主成分分析は線形回帰とは全く違います。式も違います!ご注意を。
主成分分析を実施するには、線形代数の「固有行列」を計算する方法が一般的です。が、ここでは詳しいことは省きます。
さて、主成分分析では、「どこまで次元を減らしていいの?」ということが気になります。変数は減らしたい、とはいうもののあまり次元を減らしすぎるとせっかく取得できたデータを無駄に均一にしてしまうことになりかねません。その場合、次元数を選ぶ基準としてvariance があります。varianceは 実際のデータのバリエーションと射影により失われたデータ量との比です。当然この値が少ない方がよいのですが、利用する場面ごとに適切なvarianceになるように次元数を選択しましょう。
さて、主成分分析は、データの圧縮や可視化などに応用されています。ただ、いくら変数が減る、といっても、過学習対策には利用できません!当たり前ですね。Andrew 先生によると、変数が多いと真っ先に次元を減らそうと主成分分析をする人が多いらしいのですが、そんな人に先生が一言。
まずは、そのままの生のデータで学習してみよう。次元を減らすのはそのあと!
あれ、私のことですか。ですよね。はい。
感想
とうとう、教師なし学習まできましたね。でも、教師あり学習に比べて教師なし学習は説明が少ないんですね。教師あり学習って、正解を知らないと学習させられないんです。現実問題では、何が問題で、何が正解か、が一番難しいところなのに。
次はラスト!異常検出やリコメンドエンジン、機械学習システムの構築と注意点について説明します。

