機械学習(2) - スタンフォード大学の講義から

こんにちは、馬場です。

今回は第３週、第４週の講義の内容を紹介します。

6. ロジスティック回帰

ロジスティック回帰は教師あり学習の一種で、正解が離散値となるような問題を解決するためのモデルです。
例えばこんな問題です。

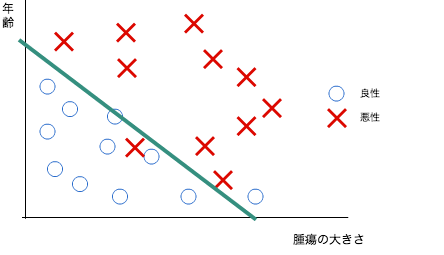
ロジスティック回帰　腫瘍の大きさと年齢から悪性かどうか予測する

モデル関数で、腫瘍の大きさと患者の年齢から腫瘍が悪性である確率を計算します。
○と×の境界に直線をひくような感じです。直線の右上にいけばいくほど悪性の可能性が高く、左下に行くほど良性の可能性が高くなります。
授業では具体的にモデルの関数とその尤度関数を紹介した後、最急降下法でパラメータを算出する手法を紹介していました。
そこで、最終的に解く式がなんと線形回帰と同じに！これなら以前作ったプログラムをロジスティック回帰問題を解くのにも使えます！！
まあそうなるように、かつそれらしくなるようにモデルを作ったんでしょうけど。
この分野は、他の自然科学より「私は世界をこうとらえているんだ」というトップダウンな感じが強い気がします。

7. 正則化

モデルをつくる場合、学習データを正しく反映したものになっているかは常に気になると思いますが、もうひとつ「過学習」という現象にも注意を払う必要があります。これは、モデルが学習データに忠実だが、他の新しいデータでの予測がうまくいかないような場合です。

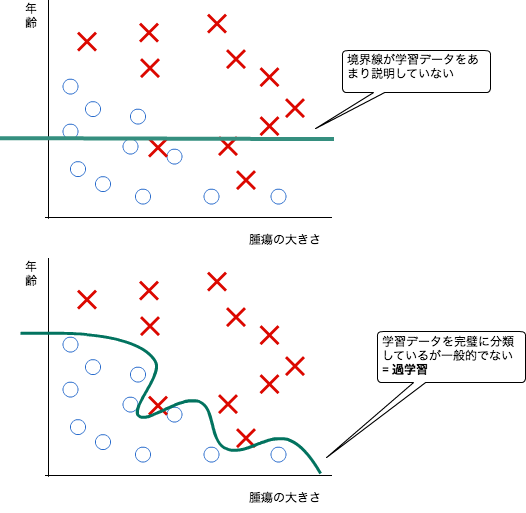
過学習の例

過学習は、変数の数が多すぎたり、モデルの形が複雑すぎたりする場合に発生します。対策としては以下の２点が考えられます。

変数を減らす。手動で変数を減らしたりモデル選択アルゴリズムを適用する。
正則化　モデル関数のパラメータを計算する際、正解と関係のない変数の影響を減らす「ペナルティ」＝正則化項を付け加える。正則化パラメータの取り方が肝。

授業では、その後正則化を実施したモデルを実際に計算していました。

7. まで終わって、Andrew 先生がうれしそうにこう言っていました。

線形回帰とロジスティック回帰だけで、かなーりいろんなことができるよ！これでいっぱいお金稼いでね！おめでとう！！

ありがとう。いっぱい稼ぎます。

8. Neural Networks

さて、線形回帰とロジスティック回帰だけでかなりいろんなことができるようになった、とはいうものの、やはり所詮モデルの形が「直線」なので、予測精度があまりよくない場合があります。
このような場合の対策として、境界を直線じゃなく多項式で表せる曲線にする方法を以前紹介していました。
ただこの方法ですと、もともとの観測変数が多いと変数が指数関数的に増加して現実的な計算量にならない、という問題があります。

そんなとき、ニューラルネットワークです。
ニューラルネットワークは、脳の働きをモデル化したものです。脳は、何か見たり、聞いたり、外部からの刺激をうけると、個々の神経細胞間で信号を伝達して、最終的に「これはりんごだ！」「誰か泣いている！」と認識したりします。このように何かの入力データに対して、ノードが編み目状につながって、データを通信して答えを導いている様子をモデル化したのが、ニューラルネットワークです。

最も単純なニューラルネットワークは以下のような形です。が、これはなんのことはない、ロジスティック回帰のモデルを形を変えて表現しただけです。

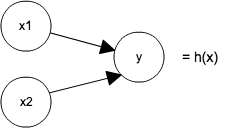
ニューラルネットワーク　ロジスティックユニット

ニューラルネットワークは、上のロジスティック回帰を組み合わせてつくったモデルです。
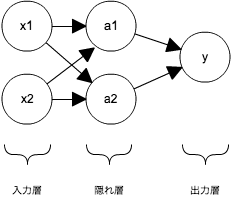
ニューラルネットワーク　例

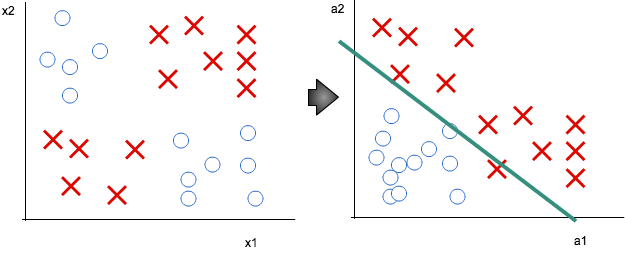
例えば、ロジスティック回帰だけでは、以下のようなデータはうまく分類できません。
XORモデル
そこで、ニューラルネットワークでa1/a2 のロジスティックユニットを適切に設定してあげると、モデルがうまくできます。
直線で分けられるように変数(a1/a2)を計算し直すような処理をやっているんだろう、と感じました。

XORも変換すると直線で分類できるようになる。

ここまであまりニューラルさを感じなかったのですが、学習データから最適なパラメータの値（ニューラルネットワークでは重みという）を計算する手法は来週紹介されるので、そこに「ニューラル」要素があるのではと期待しています。

感想

過学習に関しては、谷田さんにアドバイスをいただきました。

過学習はどんなアプローチをするにせよ、機械学習をする場合、データに偏りがあったり少なかったりした場合、常に起こり得る課題で、過学習を避ける方法は、ここに書かれているような定量的な方法（各手法によって多少違いますが）も重要ですが、本当は、種々の観測・調査によって得られた、定性的な仮説を元にモデルを組み立てることこそが、過学習に陥らないためのベターな方法であると私は考えています。

定量的手法に走りすぎると、つい、定性的な仮説が疎かになり、過去に痛い思いを何度もしました^-^;
データが十分にあるとき、安心してしまうんですよね。

想像力を働かせて、ですね。なるほど。

ロジスティック回帰の応用範囲は広い、と思いました。「○か×か」を予測する問題はすごく多いので。
ニューラルネットワークは、集合知プログラミングで読んだときはあまりよくわからなかったのですが、今回は（ここまでは）すんなり入ってきました。ロジスティック回帰からニューラルネットワークに持っていっているところや、「どういう問題を解くためのモデルか」というところをまず徹底的に説明したあと「どうやって解くか」という授業の流れが秀逸だったのではないかと思っています。
来週も楽しみです。

次回はニューラルネットワーク（解き方編）と、機械学習の応用です。